CAS系统思考③，系统循环图的核心构成

系统循环图，casual loop diagram，CLD，又称因果回路图，用于表示系统结构。

回路是系统循环图中必不可少的关键引出，没有回路，就不算一个完整的系统图。回路由变量与连接构成。

系统循环图可以帮助我们进行深入、动态及全面的思考，可以用于梳理个人思路，检视与改善心智模式，做出明智决策，设计成长引擎，寻找杠杆解，与相关人员进行交流讨论、促进共识和变革……

由两个以上的因果关系链首尾相连形成的闭合回路，就是反馈回路。在反馈回路中，原因和结果是具有相对性的，原因会影响结果，结果也会反过来影响原因。换句话说，回路中的每个要素，既是因也是果。

最简单的反馈回路例如复利模式，余额增多会导致利息增多，利息增多又会导致余额增多，从而形成复利循环。

反馈是复杂系统的本质特征，是系统运作的核心。反馈回路直接决定了系统循环图的完整性，第一个反馈回路即是正确系统图的开始。

各要素随着闭合环的每次旋转而不断得到增强，这就是正反馈，对应的回路就是增强回路。增强回路具有自我强化或弱化的趋势，可导致指数级增长或崩溃。复利模式、马太效应以及我们所追求的增长引擎等等，都是典型的增强回路。必须注意，增强回路有好、坏两个方向。

与之对应的是调节回路，该回路总是保持平衡或达到某特定目标，是稳定性的根源。调节回路普遍存在于生物系统中，例如动物的体内平衡，例如人的体温系统总是将体温维持在37℃左右。日常生活中，也可以抽象出很多常见的调节回路，例如接水这个过程，就可以形成一个调节回路。

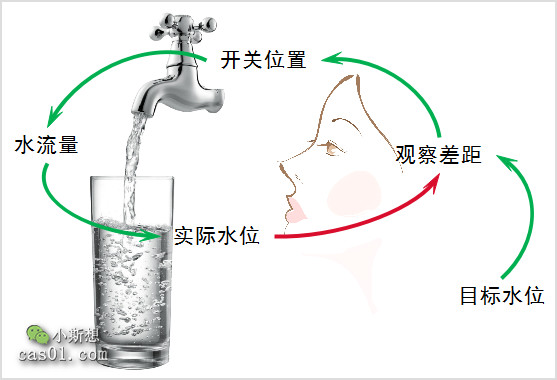
如何判断一个回路到底是增强回路还是调节回路呢？

因果连接只有两种：原因增长导致结果增长，就是S型连接；原因增长导致结果下降，就是O型连接。回路类型也只有两种：增强回路，调节回路。回路的类型取决于闭合回路中的O型连接个数：偶数个O型连接就是增强回路，奇数个则是调节回路。

闭合回路没有起点和重点，但现实中很多系统循环图，还会有另外的一类控制因素，它在闭环之外但却连接在闭环之上，这类因素被称为悬摆，比如前面那个调节回路中的“目标水位”。悬摆可以用来定义系统边界，输入悬摆可以用来确定目标，输出悬摆可用来确定结果。

现实生活中的系统，时间延迟是无所不在的。所谓延迟，指的是改变一个原因，不会立即导致结果的发生，总会经过一定的时间延迟。时间延迟会导致动态复杂性。

①. 从哪入手？从以下几个关键问题开始：最关心的问题是什么？最关键的驱动力是什么？关键成果是什么？最关键因素是什么？

②. 定义变量。弄清楚驱动力；识别关键因素，不要纠结于细枝末节；用词上保持一致性，别用动词，用名词。

③. 定义连接关系。画出因果关系链，得到反馈回路。

④. 定义系统边界。把握住相关性，只将有用的事物包括进来，可借助悬摆定义目标边界。

⑤. 坚持画图，坚持改进。从简单的问题开始，另外，没有已完成或完美的图表。